libnumerixpp  0.1.3
A Powerful C++ Library for High-Performance Numerical Computing
docs/ru/article.md File Reference

A Powerful C++ Library for High-Performance Numerical Computing. More...

Detailed Description

A Powerful C++ Library for High-Performance Numerical Computing.

Quadratic utils for mathematics.

Math utils for quadratic.

Core utils for mathematics.

Physics utils for kinematics.

Core utils for physics.

Core common utils for libnumerixpp.

  • *
    Version
    0.1.0
  • Date
    2024-09-21
  • Authors
    alxvdev
  • Copyright
    Apache 2.0 License */ #include <iostream>
    void println(std::string string) { std::cout << string << std::endl; } ```

И его заголовочного файла libnumerixpp.hpp:

```cpp #ifndef LIBNUMERIXPP_HPP #define LIBNUMERIXPP_HPP

#include <string>

#pragma once

/**

  • Print string with new line
  • Parameters
    [in]stringThe string */ void println(std::string string);
    #endif // LIBNUMERIXPP_HPP ```

Комментарии-документацию я вывожу именно в include-файлах.

# Блок ядра библиотеки Директория core/ - это базовый модуль, в котором будут содержаться некоторые основные функции нашей библиотеки.

Итак, core/common.cpp:

```cpp /**

  • *
    Authors
    alxvdev */ #include <chrono> #include <functional> #include <iostream>
    void credits(void) { std::cout << "libnumerixpp v0.1.0 - A powerful C++ Library for High-Performance Numerical Computing" << std::endl; std::cout << "Licensed by Apache License" << std::endl; std::cout << "Developed&maintained by @alxvdev" << std::endl; std::cout << std::endl; } ```

А теперь его заголовочный файл:

```cpp /**

  • *
    Authors
    alxvdev */ #ifndef LIBNUMERIXPP_COMMON_HPP #define LIBNUMERIXPP_COMMON_HPP
    #pragma once

/**

#endif // LIBNUMERIXPP_COMMON_HPP

```

## Физика Т.к. модуль физики на данный момент меньше чем модуль математики, начнем именно с него.

Создадим базовый файл physics/core.cpp:

```cpp /**

  • *
    Authors
    alxvdev */
    namespace physics { } ```

Здесь ничего на данный момент нету, просто пустой namespace physics. Позже мы его дополним.

И по традиции, physics/core.hpp:

```cpp /**

  • *
    Authors
    alxvdev */ #ifndef LIBNUMERIXPP_PHYSICS_CORE_HPP #define LIBNUMERIXPP_PHYSICS_CORE_HPP
    #pragma once

/**

#endif // LIBNUMERIXPP_PHYSICS_CORE_HPP ```

Следующий шаг - уже настоящий функционал модуля. Для примера я взял базовую кинематику. Рассмотрим файл physics/kinematics.cpp:

```cpp /**

  • *

    Authors
    alxvdev */ #include "libnumerixpp/physics/core.hpp"

    namespace physics::kinematics {

    double calculatePath(double speed, double time) { return speed * time; }

    double calculateSpeed(double path, double time) { return path / time; }

    double calculateTime(double path, double speed) { return path / speed; }

    double calculateFinalVelocity(double initial_velocity, double acceleration, double time) { return initial_velocity + acceleration * time; }

    double calculateFinalPosition(double initial_position, double initial_velocity, double acceleration, double time) { return initial_position + initial_velocity * time + 0.5 * acceleration * time * time; } } ```

Здесь вы видите 5 функций. Первые три являются разными подвидами одной формулы: S = v * t (путь равен скорости умноженной на время). А вот две оставшиеся поинтереснее:

calculateFinalVelocity высчитывает конечную скорость объекта, используя формулу: v = u + at, где:

  • v - конечная скорость (м/c)
  • u - начальная скорость (м/c)
  • a - ускорение (м/с)
  • t - время, в течение которого действовало ускорение (с)

calculateFinalPosition высчитывает конечную позицию объекта, используя формулу: s = s0 + v0 * t + 0.5 * a * t^2, где:

  • s - конечное положение
  • s0 - начальное положение
  • v0 - начальная скорость
  • a - ускорение
  • t - время

Код простой, но база сделана. Если вам понравится данная статья, я могу сделать 2 часть, где мы добавим больше функционала.

И не забудем про файл physics/kinematics.hpp:

```cpp /**

  • *
    Authors
    alxvdev */ #ifndef LIBNUMERIXPP_PHYSICS_KINEMATICS_HPP #define LIBNUMERIXPP_PHYSICS_KINEMATICS_HPP
    #pragma once

/**

  • Namespace of kinematics (physics)
  • Todo:
    Add more kinematics equations */ namespace physics::kinematics {

    /**

    • Calculates the path.
    • This function is based on basic formule: S = v * t
    • where:
    • + S - path (m)
    • + v - speed (m/s)
    • + t - time (s)
  • Parameters
    [in]speedThe speed
  • Parameters
    [in]timeThe time
  • Returns
    The path. */ double calculatePath(double speed, double time);
    /**
  • Calculates the speed.
  • This function is based on basic formule: S = v * t
  • where:
  • + S - path (m)
  • + v - speed (m/s)
  • + t - time (s)
  • Parameters
    [in]pathThe path
  • Parameters
    [in]timeThe time
  • Returns
    The speed. */ double calculateSpeed(double path, double time);
    /**
  • Calculates the time.
  • This function is based on basic formule: S = v * t
  • where:
  • + S - path (m)
  • + v - speed (m/s)
  • + t - time (s)
  • Parameters
    [in]pathThe path
  • Parameters
    [in]speedThe speed
  • Returns
    The time. */ double calculateTime(double path, double speed);
    /**
  • Calculates the final velocity.
  • This function is based on the basic kinematics equation: v = u + at
  • where:
  • + v - final velocity (m/s)
  • + u - start speed (m/s)
  • + a - accelaration (m/s^2)
  • + t - time (s)
  • Parameters
    [in]initial_velocityThe initial velocity
  • Parameters
    [in]accelerationThe acceleration
  • Parameters
    [in]timeThe time
  • Returns
    The final velocity. */ double calculateFinalVelocity(double initial_velocity, double acceleration, double time);
    /**
  • Calculates the final position.
  • This function is based on the kinematics equation: s = u*t + 0.5 * a * t^2
  • where:
  • + s - final position (m)
  • + u - start speed (m/s)
  • + a - acceleration (m/s^2)
  • + t - time (s)
  • Parameters
    [in]initial_positionThe initial position
  • Parameters
    [in]initial_velocityThe initial velocity
  • Parameters
    [in]accelerationThe acceleration
  • Parameters
    [in]timeThe time
  • Returns
    The final position. */ double calculateFinalPosition(double initial_position, double initial_velocity, double acceleration, double time); }
    #endif // LIBNUMERIXPP_PHYSICS_KINEMATICS_HPP ```

Перейдем к следующему модулю.

## Математика Итак, начнем с mathematics/core.cpp:

```cpp /**

  • *

    Authors
    alxvdev */ #include <math.h>

    namespace mathematics {

    double oldApproximatePower(double base, double exponent) { union { double d; long long i; } u = { base };

    long long magicNum = 4606853616395542500L;

    u.i = (long long)(magicNum + exponent * (u.i - magicNum));

    return u.d; }

    double binaryPower(double base, unsigned long long exponent) { double v = 1.0;

    while(exponent != 0) { if((exponent & 1) != 0) v *= base;

    base *= base; exponent >>= 1; }

    return v; }

    double fastPowerDividing(double base, double exponent) { if(base == 1.0 || exponent == 0.0) return 1.0;

    double eAbs = fabs(exponent); double el = ceil(eAbs); double basePart = oldApproximatePower(base, eAbs / el); double result = binaryPower(basePart, (unsigned long long)el);

    if(exponent < 0.0) { return 1.0 / result; }

    return result; }

    double anotherApproximatePower(double base, double exponent) { union { double d; int x[2]; } u = { base };

    u.x[1] = (int)(exponent * (u.x[1] - 1072632447) + 1072632447); u.x[0] = 0;

    return u.d; }

    double fastPowerFractional(double base, double exponent) { if(base == 1.0 || exponent == 0.0) return 1.0;

    double absExp = fabs(exponent); unsigned long long eIntPart = (long long)absExp; double eFractPart = absExp - eIntPart; double result = oldApproximatePower(base, eFractPart) * binaryPower(base, eIntPart);

    if(exponent < 0.0) return 1.0 / result;

    return result; }

    double add_percent_to_number(double number, double percentage) { double oneperc = number / 100; double result = number + (oneperc * percentage);

    return result; }

    double square_it_up(double num) { return num * num; }

    double get_square_root(double num) { if (num <= 0) return 0;

    int exp = 0;

    num = frexp(num, &exp);

    if (exp & 1) { exp–; num *= 2; }

    double y = (1 + num) / 2; double z = 0;

    while (y != z) { z = y; y = (y + num / y) / 2; }

    return ldexp(y, exp / 2); } } ```

В начале вы можете увидеть разные виды возведения числа в степень, мы их рассмотрим ниже. А вот в конце находятся более простые функции - для добавления процента к числу, возведения в квадрат, и получения квадратного корня. Функция получения квадратного корня работает так: если входное число меньше или ровно 0, возвращаем 0. Далее используем frexp() для выделения мантиссы и порядка числа num. Мантиссу помещаем в переменную num, а порядок числа - в exp. Если порядок числа exp является нечетным, то его уменьшают на 1 и мантиссу num умножают на 2. Это необходимо для того, чтобы привести число к виду, когда мантисса находится в диапазоне [0.5, 1) (от 0.5 включая до 1 не включая). Затем инициализируются две перемнные: y=начальное значение, равно среднему между 1 и мантиссой num, и z=0. Далее выполняется итеративный цикл вычисления квадратного корня. После возвращаем результат, умноженный но соответствующую степень 2, вычисленную ранее на основе порядке exp.

А теперь, чтобы перейти к методам возведения в степень, создадим mathematics/core.hpp:

```cpp /**

  • *
    Authors
    alxvdev */ #ifndef LIBNUMERIXPP_MATHEMATICS_CORE_HPP #define LIBNUMERIXPP_MATHEMATICS_CORE_HPP
    #pragma once

/**

  • If accuracy is not important to you and the degrees are in
  • the range from -1 to 1, you can use this method (see also
  • 'another' approximation: anotherApproximatePower()). This
  • method is based on the algorithm used in the 2005 game Quake
  • III Arena. He raised the number x to the power -0.5, i.e.
  • found the value: \(\frac{1}{\sqrt{x}}\)
  • Parameters
    [in]baseThe base
  • Parameters
    [in]exponentThe exponent
  • Returns
    raised value */ double oldApproximatePower(double base, double exponent);
    /**
  • Algorithm for fast exponentiation "'Another' approximation"
  • Speed increase: ~9 times. Accuracy: <1.5%. Limitations:
  • accuracy drops rapidly as the absolute value of the degree
  • increases and remains acceptable in the range [-10, 10] (see
  • also 'old' approximation: oldApproximatePower()).
  • Parameters
    [in]baseThe base
  • Parameters
    [in]exponentThe exponent
  • Returns
    raised value */ double anotherApproximatePower(double base, double exponent);
    /**
  • Algorithm: Binary exponentiation
  • Speed increase: ~7.5 times on average, the advantage remains
  • until numbers are raised to a power of 134217728, Speed
  • increase: ~7.5 times on average, the advantage remains until
  • the numbers are raised to the power of 134217728. Error:
  • none, but it is worth noting that the multiplication
  • operation is not associative for floating point numbers, i.e.
  • 1.21 * 1.21 is not the same as 1.1 * 1.1 * 1.1 * 1.1,
  • however, when compared with standard functions, errors do not
  • arise, as mentioned earlier. Restrictions: the degree must be
  • an integer not less than 0
  • Parameters
    [in]basebase
  • Parameters
    [in]exponentexponent
  • Returns
    raised value */ double binaryPower(double b, unsigned long long e);
    /**
  • Algorithm: "Dividing fast power"
  • Speed increase: ~3.5 times. Accuracy: ~13%. The code below
  • contains checks for special input data. Without them, the
  • code runs only 10% faster, but the error increases tenfold
  • (especially when using negative powers).
  • Parameters
    [in]baseThe base
  • Parameters
    [in]exponentThe exponent
  • Returns
    raised value */ double fastPowerDividing(double base, double exponent);
    /**
  • Algorithm: "Fractional fast power"
  • Speed increase: ~4.4 times. Accuracy: ~0.7%
  • Parameters
    [in]baseThe base
  • Parameters
    [in]exponentThe exponent
  • Returns
    raised value */ double fastPowerFractional(double base, double exponent);
    /**
  • Adds a percent to number.
  • Parameters
    [in]numberThe number
  • Parameters
    [in]percentageThe percentage
  • Returns
    number */ double add_percent_to_number(double number, double percentage);
    /**
  • Gets the number square (N^2).
  • Parameters
    [in]numThe number
  • Returns
    The number square. */ double square_it_up(double num);
    /**
  • Gets the square root.
  • Parameters
    [in]numThe number
  • Returns
    The square root. */ double get_square_root(double num); }
    #endif // LIBNUMERIXPP_MATHEMATICS_CORE_HPP ```

### Заново изобретаем std::pow В этом разделе я покажу реализации нескольких нестандартных алгоритмов для возведения числа в степень. Реализация и описание способ взяты из этой статьи на хабре.

Скорость алгоритмов сравнивается с std::pow.

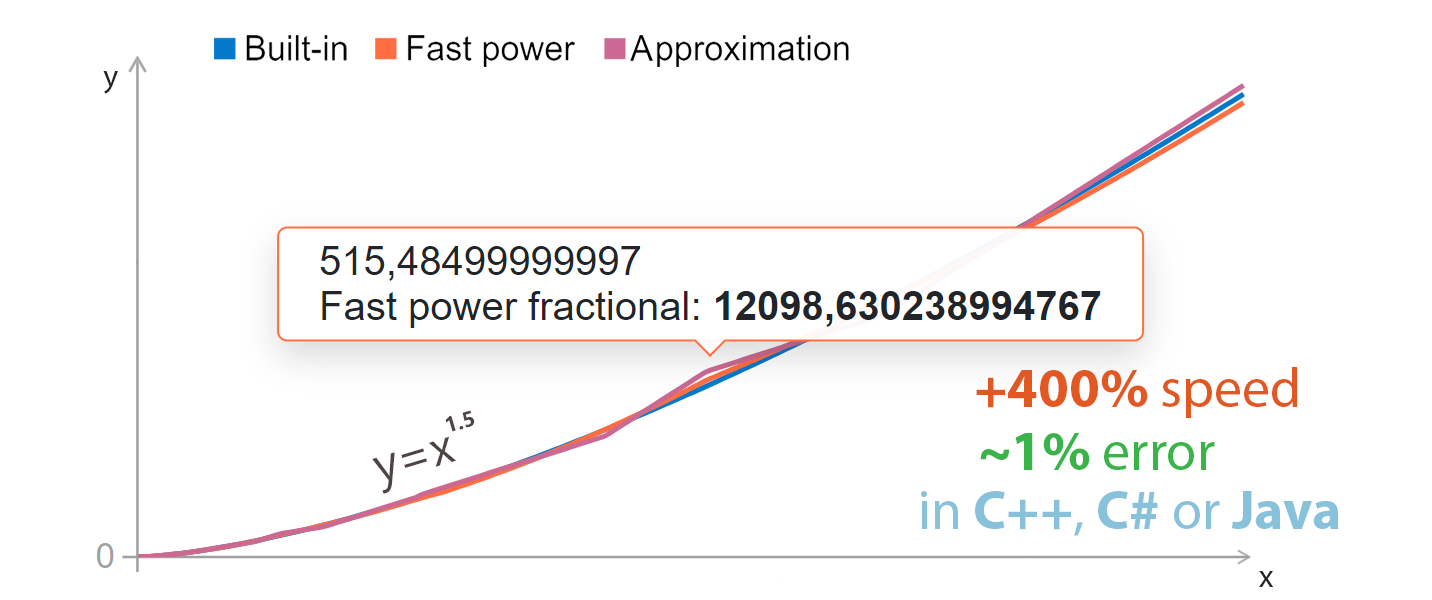
#### Алгоритм: "Старая аппроксимация" Этот метод основан на алгоритме, использованном в игре Quake III Arena 2005 года. Он возводил число x в степень -0.5.

  • Увеличение скорости: в ~11 раз.
  • Погрешность: <2%.
  • Ограничения: приемлемая точность только для степеней от -1 до 1.

```cpp double oldApproximatePower(double base, double exponent) { union { double d; long long i; } u = { base };

long long magicNum = 4606853616395542500L;

u.i = (long long)(magicNum + exponent * (u.i - magicNum));

return u.d; } ```

magicNum = это магическое число. Вы можете узнать о нем подробнее в этой статье.

#### Алгоритм: Бинарное возведение в степень Увеличение скорости: в среднем в ~7.5 раз, преимущество сохраняется до возведения чисел в степень 134217728.

Погрешность: нет, но стоит отметить, что операция умножения не ассоциативна для чисел с плавающей точкой, т.е. 1.21 * 1.21 не то же самое, что 1.1 * 1.1 * 1.1 * 1.1, однако при сравнении со стандартными функциями погрешности, как уже сказано ранее, не возникает.

Ограничения: степень должна быть целым числом не меньше 0

```cpp double binaryPower(double base, unsigned long long exponent) { double v = 1.0;

while(exponent != 0) { if((exponent & 1) != 0) v *= base;

base *= base; exponent >>= 1; }

return v; } ```

Широко известный алгоритм для возведения любого числа в целую степень с абсолютной точностью. Принцип действия прост: есть целая степень e, чтобы получить число b в этой степени нужно возвести это число во все степени 1, 2, 4, … 2n (в коде этому соответствует base *= base), каждый раз сдвигая биты e вправо (e >>= 1) пока оно не равно 0 и тогда, когда последний бит e не равен нулю ((exponent & 1) != 0), домножать результат v на полученное base.

#### Алгоритм: "Делящая быстрая степень" Увеличение скорости: в ~3.5 раз

Погрешность: ~13%

Примечание: в коде ниже присутствуют проверки для особых входных данных. Без них код работает всего на 10% быстрее, но погрешность возрастает в десятки раз (особенно при использовании отрицательных степеней).

```cpp double fastPowerDividing(double base, double exponent) { if(base == 1.0 || exponent == 0.0) return 1.0;

double eAbs = fabs(exponent); double el = ceil(eAbs); double basePart = oldApproximatePower(base, eAbs / el); double result = binaryPower(basePart, (unsigned long long)el);

if(exponent < 0.0) { return 1.0 / result; }

return result; } ```

#### Алгоритм: "Дробная быстрая степень" Увеличение скорости: в ~4.4 раза

Погрешность: ~0.7%

```cpp double fastPowerFractional(double base, double exponent) { if(base == 1.0 || exponent == 0.0) return 1.0;

double absExp = fabs(exponent); unsigned long long eIntPart = (long long)absExp; double eFractPart = absExp - eIntPart; double result = oldApproximatePower(base, eFractPart) * binaryPower(base, eIntPart);

if(exponent < 0.0) return 1.0 / result;

return result; } ```

По сути, любое число состоит из суммы двух частей: целой и дробной. Целую можно использовать для возведения основания в степень при помощи бинарного возведения, а дробную - при помощи “старой” аппроксимации.

#### Алгоритм: "Другая аппроксимация" Увеличение скорости: в ~9 раз

Погрешность: <1.5%

Ограничения: точность стремительно падает при повышении абсолютного значения степени и остается приемлемой в промежутке [-10, 10]

```cpp double anotherApproximatePower(double base, double exponent) { union { double d; int x[2]; } u = { base };

u.x[1] = (int)(exponent * (u.x[1] - 1072632447) + 1072632447); u.x[0] = 0;

return u.d; } ```

#### Сравнение

Каждый из перечисленных методов дает различную точность и скорость. Поэтому, прежде чем использовать стандартную функцию возведения в степень, стоит проанализировать какие у вас будут входные данные, и насколько вам важна точность. Выбор правильного метода может существенно ускорить работу вашей программы.

### Квадратные уравнения Продолжим улучшение модуля математики - на этот раз займемся квадратными уравнениями.

Создадим файл mathematics/quadratic_equations.cpp:

```cpp /**

  • *

    Authors
    alxvdev */ #include <vector> #include "libnumerixpp/mathematics/core.hpp"

    namespace mathematics::quadratic {

    double calculateDiscriminant(double a, double b, double c) { double d = mathematics::square_it_up(b) - 4 * a * c;

    return d; }

    std::vector<double> calculateRootsByDiscriminant(double discriminant, double a, double b) { std::vector<double> roots;

    if (discriminant > 0) { double x1 = (-b + get_square_root(discriminant)) / (2 * a); double x2 = (-b - get_square_root(discriminant)) / (2 * a);

    roots.push_back(x1); roots.push_back(x2); } else if (discriminant == 0) { double x1 = -b + get_square_root(discriminant) / (2 * a); roots.push_back(x1); }

    return roots; }

    std::vector<double> getRootsByVietaTheorem(double a, double b, double c) { std::vector<double> roots;

    if (a == 0) return roots;

    double roots_sum = -(b / a); double roots_mul = c / a;

    roots.push_back(roots_sum); roots.push_back(roots_mul);

    return roots; } } ```

Функция calculateDiscriminant высчитывает дискриминант по формуле D = b^2 - 4ac.

Функция calculateRootsByDiscriminant высчитывает корни уравнения. На вход принимает дискриминант, переменные a и b. На выходе возвращает vector (массив с неясным количеством элементов, проще говоря) типа double. Если дискриминант больше 0, то корня два, высчитываем их по формуле: -b +- квадратный корень из дискриминанта / 2a. Если дискриминант равен 0, то корень 1. А если дискриминант равен нулю - то корней нет.

Функция getRootsByVietaTheorem "получает корни" по теореме Виета. Теорема Виета гласит, если a != 0, значит: x1 + x2 = - b / a И x1 * x2 = c / a. В данной функции мы как раз и получаем их. А вот реализацию поиска корней я решил пока не делать.

И следующим шагом мы создаем файл mathematics/quadratic_equations.hpp:

```cpp /**

  • *
    Authors
    alxvdev */ #ifndef LIBNUMERIXPP_MATHEMATICS_QUADRATIC_EQUATIONS_HPP #define LIBNUMERIXPP_MATHEMATICS_QUADRATIC_EQUATIONS_HPP
    #pragma once

#include <vector> #include "libnumerixpp/mathematics/core.hpp"

/**

  • mathematics utils for quadratic equations and other
  • Based on discriminant formula: \(b^{2} - 4ac\)
  • Parameters
    [in]aa
  • Parameters
    [in]bb
  • Parameters
    [in]cc
  • Returns
    The discriminant. */ double calculateDiscriminant(double a, double b, double c);
    /**
  • Calculates the roots by discriminant.
  • Calculate the roots by discriminant \(\frac{-b +- * \sqrt{D}}{2a}\). D > 0 = 2 roots, D == 0 = 1 root, D < 0 = 0
  • roots.
  • Parameters
    [in]discriminantThe discriminant
  • Parameters
    [in]aa
  • Parameters
    [in]bb
  • Returns
    The roots by discriminant. */ std::vector<double> calculateRootsByDiscriminant(double discriminant, double a, double b);
    /**
  • Gets the roots by vieta theorem.
  • Parameters
    [in]aa
  • Parameters
    [in]bb
  • Parameters
    [in]cc
  • Returns
    The roots by vieta theorem. */ std::vector<double> getRootsByVietaTheorem(double a, double b, double c); }
    #endif // LIBNUMERIXPP_MATHEMATICS_QUADRATIC_EQUATIONS_HPP ```

Мы закончили разработку модулей. Пора перейти к примерам.

## Примеры В данной части статьи мы создадим файлы example-1.cpp и example-2.cpp в директории examples. В этих файлах будут содержаться примеры работы библиотеки.

Напишем example-1.cpp, где мы будем тестировать модуль физики:

```cpp #include <iostream> #include "libnumerixpp/libnumerixpp.hpp" #include "libnumerixpp/core/common.hpp" #include "libnumerixpp/physics/core.hpp" #include "libnumerixpp/physics/kinematics.hpp"

int main() { credits(); say_hello("LIBNUMERIXPP");

double speed = 10.0; double time = 5.0;

double path = physics::kinematics::calculatePath(speed, time); speed = physics::kinematics::calculateSpeed(path, time); time = physics::kinematics::calculateSpeed(path, speed);

std::cout << "Calculate: speed=" << speed << "m/s" << "; time=" << time << "s" << "; path=" << path << "m" << std::endl;

double finalVelocity = physics::kinematics::calculateFinalVelocity(10.0, 10.0, 10.0); std::cout << "final velocity (10.0, 10.0, 10.0) = " << finalVelocity << std::endl;

double finalPosition = physics::kinematics::calculateFinalPosition(10.0, 10.0, 10.0, 10.0); std::cout << "final position (10.0, 10.0, 10.0, 10.0) = " << finalVelocity << std::endl;

return 0; } ```

При сборке данный файл выведет:

``` libnumerixpp v0.1.0 - A powerful C++ Library for High-Performance Numerical Computing Licensed by Apache License Developed&maintained by @alxvdev

LIBNUMERIXPP Calculate: speed=10m/s; time=5s; path=50m final velocity (10.0, 10.0, 10.0) = 110 final position (10.0, 10.0, 10.0, 10.0) = 110 ```

А теперь второй файл - example-2.cpp, где будут примеры использования модуля математики:

```cpp #include <iostream> #include <vector> #include "libnumerixpp/libnumerixpp.hpp" #include "libnumerixpp/core/common.hpp" #include "libnumerixpp/mathematics/core.hpp" #include "libnumerixpp/mathematics/quadratic_equations.hpp"

int main() { credits(); println("LIBNUMERIXPP");

// SQUARE AND SQR //

double num = 100.0; double num_sq = mathematics::square_it_up(num); double num_sqr = mathematics::get_square_root(num); std::cout << "Square " << num << ": " << num_sq << std::endl; std::cout << "Square root " << num << ": " << num_sqr << std::endl;

std::cout << std::endl;

// CALCULATE QUADRATIC EQUATION BY DISCRIMINANT //

double a = -2; double b = 5; double c = 5;

double d = mathematics::quadratic::calculateDiscriminant(a, b, c); std::vector<double> roots = mathematics::quadratic::calculateRootsByDiscriminant(d, a, b);

std::cout << "Quadratic Equation: a=" << a << "; b=" << b << "; c=" << c << std::endl; std::cout << "D=" << d << std::endl; std::cout << "Roots:" << std::endl;

for (double root : roots) { std::cout << root << std::endl; }

std::cout << std::endl;

// PERCENTAGE //

double nump = mathematics::add_percent_to_number(100.0, 10.0); std::cout << "100+10%: " << nump << std::endl;

std::cout << std::endl;

// POWER / Algorithms for fast exponentiation //

double bestPowVal = 100; double pow_results[5] = { mathematics::oldApproximatePower(10.0, 2.0), mathematics::anotherApproximatePower(10.0, 2.0), mathematics::binaryPower(10.0, 2), mathematics::fastPowerDividing(10.0, 2.0), mathematics::fastPowerFractional(10.0, 2.0) };

std::cout << "0 oldApproximatePower : base 10 exponent 2: " << pow_results[0] << std::endl; std::cout << "1 anotherApproximatePower: base 10 exponent 2: " << pow_results[1] << std::endl; std::cout << "2 binaryPower : base 10 exponent 2: " << pow_results[2] << std::endl; std::cout << "3 fastPowerDividing : base 10 exponent 2: " << pow_results[3] << std::endl; std::cout << "4 fastPowerFractional : base 10 exponent 2: " << pow_results[4] << std::endl;

for (int i = 0; i < sizeof(pow_results) / sizeof(pow_results[0]); i++) { double error = bestPowVal - pow_results[i];

std::cout << "POW Algorithm #" << i << ": error=" << error << std::endl; }

return 0; } ```

При компиляции данный файл выведет:

``` libnumerixpp v0.1.0 - A powerful C++ Library for High-Performance Numerical Computing Licensed by Apache License Developed&maintained by @alxvdev

LIBNUMERIXPP Square 100: 10000 Square root 100: 10

Quadratic Equation: a=-2; b=5; c=5 D=65 Roots: -0.765564 3.26556

100+10%: 110

0 oldApproximatePower : base 10 exponent 2: 100.673 1 anotherApproximatePower: base 10 exponent 2: 99.711 2 binaryPower : base 10 exponent 2: 100 3 fastPowerDividing : base 10 exponent 2: 100 4 fastPowerFractional : base 10 exponent 2: 96.3496 POW Algorithm #0: error=-0.672563 POW Algorithm #1: error=0.289001 POW Algorithm #2: error=0 POW Algorithm #3: error=0 POW Algorithm #4: error=3.65044 ```

Вот и все. С программированием мы закончили - настало очередь украшательств.

# Украшаем репозиторий Итак, любой проект будет привлекательнее с грамотно оформленным README. У меня в проекте он выглядит так.

Документация поможет пользователям и разработчикам. Да, если им сильно нужно - они могут и просто скачать или почитать код, но многих отсутствие нормальной документации или хотя-бы нормального README файла отпугивает. Что вы бы выбрали - хорошо заполненный и документированный репозиторий или такой же репозиторий, но без какой либо информации? Я думаю, ответ очевиден.

Давайте разберем README поэтапно. Начнем с шапки:

```md # libnumerixpp

A Powerful C++ Library for High-Performance Numerical Computing


> [!CAUTION] > At the moment, libnumerixpp is under active development (alpha), many things may not work, and this version is not recommended for use (all at your own risk).

libnumerixpp is a powerful, cross-platofrm C++ library designed for high-performance numerical computing in the domains of physics, mathematics, and computer science.

You can join to our small russian telegram blog.

You can view docs for libnumerixpp here. ```

Вверху мы указываем заголовок, название проекта. Ниже описание и бейджи. Бейджи нужны для общей статистики проекта - лицензия, язык, звезды и т.д. Замените /alxvdev/libnumerixpp на свой юзернейм и репозиторий.

После мы вставляем предупреждение в виде цитаты, что проект в стадии разработки и может быть не стабилен.

Ниже также детали, и другие важные вещи, на которые сразу стоит обратить внимания. У меня это ссылка на телеграм-канал и на документацию.

Идем дальше:

```md ## Key Features

  • Extensive Functionality: libnumerixpp provides a wide range of functions coverint the core areas of mathematics, physics, and computer science, including:
    • Mathematics: linear algebra, calculus, geometry
    • Physics: kinematics, mechanics, thermodynamics, electronics
    • Computer Science: algorithms, numerical methods, data processing
  • High Performance: The library is optimized for maximum performance, leveraging modern techniques such as parallel computing and vectorization
  • Cross-platform Support: libnumerixpp supports major operating systems (Windows, Linux, macOS) and can be compiled using various compilers (GCC, CLANG, MSVC).
  • Ease of Use: A simple and intuitive API, comprehensive documentation, and numerous examples facilitate the integration of the library into your projects.
  • Modular Architecture: libnumerixpp is designed with a modular structure, allowing selective compilation of only the required components.
  • Extensibility: The library is open to the developer community, who can contribute improvements and additions. ```

Основные возможности. Здесь можно перечислить, что может ваш проект, какие у него преимущества.

Далее вы можете также создавать разные блоки, рассказывающие, например, о структуре.

Желательно еще дать инструкции по установке и сборке. Посмотрите, как сделано в моем репозитории.

Следующим шагом я бы сделал ссылки на примеры использование, зависимости и инструменты, а также раздел документации и поддержки:

```md ## Examples Below you can see examples of using libnumerixpp in your project. Also, you can view examples dir.

### example-1 Speed, Time, Path Source code: example-1.cpp

This example shows how to calculate the speed, path, and time using the physics::kinematics.

### example-2 Math, Quadratic and math Source code: example-2.cpp

This example shows how to calculate the quadratic equations, discriminant, squares using the mathematics and mathematics::quadratic.

## Tools and Dependencies linumerixpp utilizes the following tools and libraries:

  • CMake: Cross-platform build system
  • Doxygen: Documentation generation

## Documentation Detailed documentation, including user guides, API reference, and code examples, is available in the docs. Or you can see articles or additional info in en docs dir or ru docs dir.

If you have any questions, suggestions, or encounter issues, please create a new issue in the repository. We'll be happy to assist you and improve the library.

You can also write to me on Telegram: @alexeev_dev

libnumerixpp is an Open Source project, and it only survives due to your feedback and support!

Project releases are available at this link. ```

И в самом конце можно указать копирайты:

```md ## Copyright libnumerixpp is released under the [Apache License 2.0](LICENSE).

Copyright © 2024 Alexeev Bronislav. All rights reversed. ```

Я хочу сказать, что это не требования, а мои рекомендации. Вы можете сделать по другому.

И небольшое наставление по коммитам. По некоторым правилам, коммит должен быть в повелительном наклонении, потому что это, как бы указание разработчику, что надо делать. Но это не указание, это также рекомендации, вы вольны использовать что хотите (или что захочет ваша команда).

## Описание коммитов | Название | Описание | |-------—|--------------------------------------------------------------—| | build | Сборка проекта или изменения внешних зависимостей | | sec | Безопасность, уязвимости | | ci | Настройка CI и работа со скриптами | | docs | Обновление документации | | feat | Добавление нового функционала | | fix | Исправление ошибок | | perf | Изменения направленные на улучшение производительности | | refactor | Правки кода без исправления ошибок или добавления новых функций | | revert | Откат на предыдущие коммиты | | style | Правки по кодстайлу (табы, отступы, точки, запятые и т.д.) | | test | Добавление тестов |

Пример:

```bash git commit -m "feat: add line output" # en, добавьте вывод строки git commit -m "feat: добавьте вывод строки" # ru ```

Больше информации об оформлении репозитория вы можете увидеть в моей старой статье.

—

Вот и все. Минимальный комплект минимальной библиотеки. Надеюсь, я сподвиг вас к чему-то большему. Пишите, творите, публикуйте!

# Заключение Спасибо за внимание! Это был довольно интересный опыт для меня, т.к. это мой первый большой проект на языке C++, где я попытался его изучить более подробно.

Если у вас есть замечания по статье или по коду - пишите, наверняка есть более опытный и профессиональный программист на C++, который может помочь как и читателям статьи, так и мне.

Ссылка на мой репозиторий реализации командного интерпретатора здесь.

Буду рад, если вы присоединитесь к моему небольшому телеграм-блогу. Анонсы статей, новости из мира IT и полезные материалы для изучения программирования и смежных областей.

P.S. вы можете прорекламировать свою библиотеку в комментариях, если она интересная и может кому-то пригодиться.

## Источники